
- 12 VOLT POWER CONVERTER AC TO DC DRIVERS
- 12 VOLT POWER CONVERTER AC TO DC DRIVER
- 12 VOLT POWER CONVERTER AC TO DC PLUS
Tried up to 17 V DC to take the sinewave peak into account.
12 VOLT POWER CONVERTER AC TO DC DRIVER
I've got some good comments below on solutions to power my lights - but still interested in hearing if anyone has used low-cost PSW driver boards.
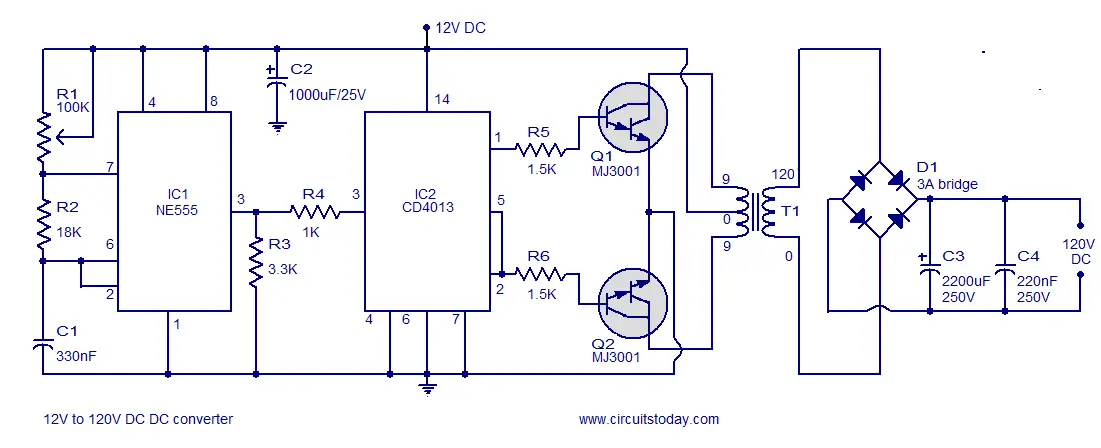
Can anyone share their experience of trying to do something similar?
12 VOLT POWER CONVERTER AC TO DC DRIVERS
I’ve been looking at single board drivers like Sunyima’s EGS002 module using their EG8010 controller chip. I was wondering if there are simpler approaches, especially modular ones. I only need a 20 W output, but haven't found any low voltage low power inverters. While this started in response to a lighting challenge, it's now a more generic enquiry. A MSW/square wave output may damage components over time, and as I said, these lights are expensive. And I'd prefer the output to be pure sine wave - at a low (50 to 60 Hz) frequency, as I know the lights will work then.
12 VOLT POWER CONVERTER AC TO DC PLUS
Intellectual curiosity took hold, and wondered if I could make a simple low voltage 12 V DC to 12 V AC 50/60 Hz PSW converter based on a modern PSW inverter control chip – plus I wouldn’t need such high-voltage components for the power stage and keeping everything LV makes it inherently safer.Īs everything is off-grid and solar/battery powered, I'm looking for high-efficiency solutions. I have an electronics background and designed stuff many years ago. And this may be the easiest and most cost-effective solution - but it's not ideal. I could convert 12 V DC to 120/230 V AC using a cheap commercial inverter then transform down again to 12 V AC (or possibly replace the inverter’s output transformer). There's no marking on the lights identifying them, and my local supplier isn't helping with this. These pool lights are too $$$ expensive – and sealed – for me to tear down. There's clearly some AC coupling involved. I tried up to 17 V DC just in case the lights relied on some peak threshhold detection, without success. For whatever reason my pool lights can't. Most normal “AC” LED lights have a bridge rectifier on the input, so can run from DC. While they work fine using 12 V AC, they don't work off the battery. This equation can provide a good starting point for practical applications.Ĭonverting AC to DC voltage is quite simple mathematically and provides a basis for understanding the necessary conversions to successfully power DC devices from a standard AC supply from the power distribution grid.This started with me trying to power 12 V AC LED swimming pool lights - which are always spec’d as AC for historical (and consequently safety certification) reasons - from a hefty 12 V DC leisure battery. Remember, of course, that in a real-life application, you’ll need to account for losses due to inefficiency in the conversion. With this information, we can convert the AC supply from the power grid to the appropriate voltage to power the device. This equation also allows us to work backward from the device, knowing its DC power requirement, to calculate the necessary input AC.

As a theoretical example, an incandescent light bulb will grow equally brightly on 141V AC (peak voltage) and 100V DC, since we express the RMS of 141V peak as: We can use the RMS equation above to determine and allow the conversion of AC to power DC devices.

Unfortunately, only hypothetical conversions maintain 100 percent efficiency. It is important to note that this determines the theoretical DC voltage equivalent based on the peak AC voltage, not the exact DC voltage that will result from any real-life conversion. Divide the peak voltage by the square root of two to obtain the RMS voltage, which is equivalent to the required DC voltage. If we know the peak voltage of an AC, we can quickly figure out the necessary DC voltage. RMS for a standard AC waveform is equal to the peak voltage divided by the square root of two, as shown in this RMS to DC formula: This is possible since we presume the wave to be identical each period. In the case of typical sinusoidal AC waveforms, the RMS over all time is equal to the RMS of one period of the wave. RMS stands for root mean square and refers to the square root of the average (arithmetic mean) of the squares of all values in the set. In general, we express DC voltage as AC RMS voltage. Fortunately, working out the mathematical conversion is quite simple. Physically converting alternating current (AC) power to direct current (DC) power involves several steps and a device called a rectifier.


 0 kommentar(er)
0 kommentar(er)
